Az aranymetszés
Az ikozaéder és a dodekaéder paramétereit az úgynevezett „aranytéglalap” – ra vezetjük vissza.
Aranymetszésnek nevezzük egy szakasz két részre osztását úgy, hogy a nagyobbik és a kisebbik részek aránya megegyezik az eredeti szakasz és a nagyobbik rész arányával. Ezt az arány pedig a görög „tau” – val jelöljük: A „tau” hasonlóan a már ismert „pi” –hez, egy írracionális szám, melynek értéke állandó. Ez azt jelenti, hogy ha például a nagyobbik részt a-val, a kisebbik részt pedig b-vel jelöljük, akkor:
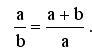
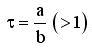
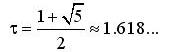
![]()
Az aranymetszés szabályából számunkra az aranytéglalap fontos, ami olyan speciális téglalap, melynek oldalai úgy aránylanak egymáshoz, mint ahogyan a két oldal összege a nagyobbik oldalhoz. A két oldal aránya tehát az 1,618034… értékű „tau”.
Kicsinyítése
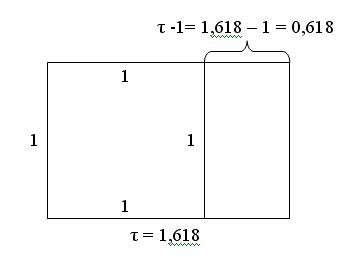
Ha egy aranytéglalapból levágunk egy a rövidebbik oldalával egyező oldalhosszú négyzetet, akkor a megmaradt téglalap hasonló lesz az eredetihez. Az egyik oldalának értéke 1 lesz, míg a másik oldala
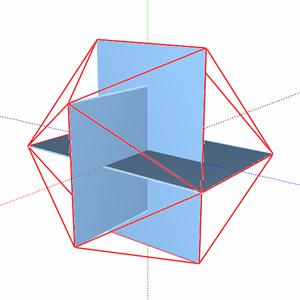
Ikozaéder
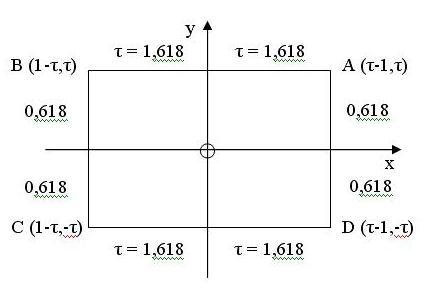
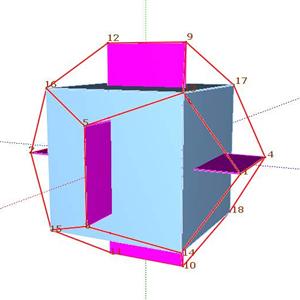
Az ikozaéder váza három, páronként egymásra merőleges aranytéglalap. Csúcsai pedig az aranytéglalapok csúcsai.
Nagyítása
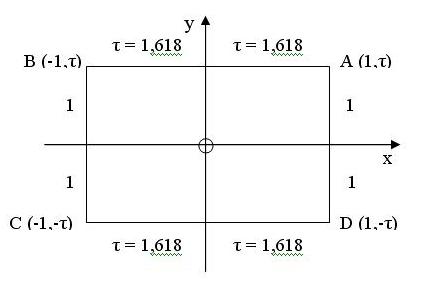
Ha mindkét oldalát kétszeresére növeljük, természetszerűen ismét aranytéglalapot kapunk, ami az eredetihez hasonló. Oldalai 2 egység és 2τ lesznek. A könnyebb láthatóság kedvéért helyezzük ezt síkbeli derékszögű koordinátarendszerbe:
Dodekaéder
A dodekaéder téglalapok némiképp eltérnek az ikozaéderhez szükséges aranytéglalapoktól.
Oldalhosszúságukhoz ezúttal nem csupán τ = 1,618034 a értékre lesz szükségünk, hanem az egységnyi téglalap levágásával keletkezett τ – 1 = 0,618034 értékre is. Az így keletkezett téglalap valamivel keskenyebb a korábban megismert téglalaphoz képest (annak 2 x 1, ennek 2 x 0,618034 az élhosszúsága).